Background

In recent years the Hough transform and the related Radon transform have received much attention. These two transforms are able to transform two dimensional images with lines into a domain of possible line parameters, where each line in the image will give a peak positioned at the corresponding line parameters. This have lead to many line detection applications within image processing, computer vision, and seismics.

Several definitions of the Radon transform exists, but the are related, and a very popular form expresses lines in the form rho=x*cos(theta)+y*sin(theta), where theta is the angle and rho the smallest distance to the origin of the coordinate system. As shown in the two foloowing definitions (which are identical), the Radon transform for a set of parameters (rho,theta) is the line integral through the image g(x,y), where the line is positioned corresponding to the value of (rho,theta). The delta() is the Dirac delta function which is infinite for argument 0 and zero for all other arguments (it integrates to one), and in digital versions the Kronecker delta is used.

Using this definition an image containing two lines are transformed into the Radon transform shown to the right

It can be seen that two very bright spots are found in the Radon transform, and the positions shown the parameters of the lines in the original image. A simple thresholding algorithm could then be used to pick out the line parameters, and given that the transform is linear many lines will just give rise to a a set of distinct point in the Radon domain. In my Ph.D. thesis the relationship with the Hough transform is investigated, and it is shown that the Radon transform and the Hough transform are related but NOT the same.

Noise

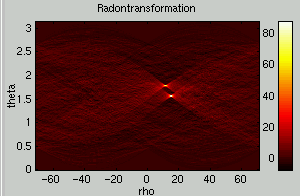
The very strong property of the Radon transform is the ability to extract lines (curves in general) from very noise images as shown below. Theoretically results regarding the influence of noise can be found in Chapter 5 of my Ph.D. thesis.

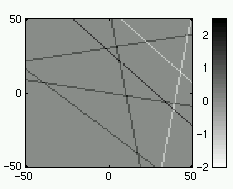
In general many lines hidden in an image can be transformed into a set of peaks, where the value in the Radon domain (to the right) reflect the value on the individual lines. From the Radon transform, shown to the right, it can be seen that crossing lines makes no problem.

The Generalized Radon transform

Last modified: Apr. 7, 1997.

You are the visitor since September 6 1996.

To Peter Toft's homepage